M. Iterativos

Definición:

Se denominan métodos iterativos o métodos de aproximaciones sucesivas a los que consisten en la obtención de una sucesión de valores que converjan a la solución de nuestro problema.

Veremos en primer lugar dos de los métodos iterativos más conocidos: el método de Jacobi y el método de Gauss-Seidel.

Método de Jacobi

EJEMPLO

Con un vector inicial:

x1=0

x2=0

x3=0

Resolver por el método de Jacobi, el siguiente sistema de ecuaciones.

6x1 + 2x2 + x3 = 22

-x1  + 8x2 + 2x3 = 30

x1 - x2 + 6x3 = 23

Solución:

1. Despejamos la variable x de cada una de las ecuaciones como sigue:

x1 = (22 - 2x2 - x3)/6

x2 = (30 + x1 - 2x3)/8

x3 = (23 - x1 + x2)/6

2. Para un vector inicial (0 ; 0 ; 0) hallo los valores de x1, x2, x3.

x1 = (22 - 2(0) - (0))/6

x2 = (30 + (0) - 2(0))/8

x3 = (23 - (0) + (0))/6

3. Teniendo para nuestra primera iteración los siguientes valores:

x1 = 3.66                            x2 = 3.75                                   x3 = 3.83 

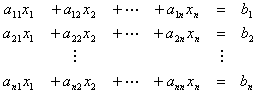
Método de Gauss-Seidel

El método de Gauss-Seidel es un método iterativo y por lo mismo resulta ser bastante eficiente. Se comienza planteando el sistema de ecuaciones con el que se va a trabajar:

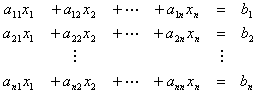
De la ecuación 1 despejar x1, de la ecuación 2 despejar x2, …, de la ecuación n despejar xn. Esto da el siguiente conjunto de ecuaciones:

EJEMPLO: Usar el método de Gauss-Seidel para aproximar la solución del sistema:

hasta que 

SOLUCIÓN:

Primero se despejan las incógnitas x1, x2 y x3 de las ecuaciones 1, 2 y 3 respectivamente. Se tiene:

Estas últimas son el juego de fórmulas iterativas que se estará utilizando.

Se comienza el proceso iterativo sustituyendo los valores de x2 = x3 = 0 en la primera ecuación, para calcular el valor de x1:

Ahora se sustituye  y x3 = 0 en la segunda ecuación para obtener x2:

Ahora se sustituye  y  en la tercera ecuación para obtener x3:

Así se tiene la primera aproximación a la solución del sistema:

Puesto que todavía no se puede calcular ningún error aproximado, se repite el proceso pero ahora con los últimos datos obtenidos para las incógnitas:

Sustituyendo  y  en la ecuación 1 se obtiene  Sustituyendo y  en la ecuación 2 se obtiene  finalmente, sustituyendo  y  en la ecuación 3 se obtiene . Es así como se tiene la segunda lista de valores de aproximación a la solución del sistema:

Ahora se pueden calcular los errores absolutos para cada una de las incógnitas:

Puesto que no se ha logrado el objetivo, se debe repetir el mismo proceso con los últimos valores obtenidos de cada una de las incógnitas. Nótese que aunque el error aproximado  ya cumple con ser menor al 1%, esto se debe cumplir para los tres errores aproximados. Por lo tanto se repite el mismo proceso. Omitiendo los pasos intermedios, se obtiene:

En este caso se tienen los siguientes errores aproximados:

Se puede observar que ahora se ha cumplido el objetivo para cada uno de los errores aproximados. Por lo tanto, se concluye que la solución aproximada es: