Newton Raphson

En análisis numérico, el método de Newton (conocido también como el método de Newton-Raphson o el método de Newton-Fourier) es un algoritmo eficiente para encontrar aproximaciones de los ceros o raíces de una función real. También puede ser usado para encontrar el máximo o mínimo de una función, encontrando los ceros de su primera derivada.

DESCRIPCIÓN 
El método de Newton-Raphson es un método abierto, en el sentido de que su convergencia global no está garantizada. La  única manera de alcanzar la convergencia es seleccionar un valor inicial lo suficientemente cercano a la raíz buscada. Así, se ha de comenzar la iteración con un valor razonablemente cercano al cero (denominado punto de arranque o valor supuesto). La relativa cercanía del punto inicial a la raíz depende mucho de la naturaleza de la propia función; si ésta presenta múltiples puntos de inflexión o pendientes grandes en el entorno de la raíz, entonces las probabilidades de que el algoritmo diverja aumentan, lo cual exige seleccionar un valor supuesto cercano a la raíz. Una vez que se ha hecho esto, el método linealiza la función por la recta tangente en ese valor supuesto. La abscisa en el origen de dicha recta será, según el método, una mejor aproximación de la raíz que el valor anterior. Se realizarán sucesivas iteraciones hasta que el método haya convergido lo suficiente. f'(x)= 0 Sea f : [a, b] -> R función derivable definida en el intervalo real [a, b]. Empezamos con un valor inicial x0 y definimos para cada número natural n
x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}.
Donde f ' denota la derivada de f.
Nótese que el método descrito es de aplicación exclusiva para funciones de una sola variable con forma analítica o implícita conocible. Existen variantes del método aplicables a sistemas discretos que permiten estimar las raíces de la tendencia, así como algoritmos que extienden el método de Newton a sistemas multivariables, sistemas de ecuaciones, etc.


ALGORITMO
Tres son las formas principales por las que tradicionalmente se ha obtenido el algoritmo de Newton-Raphson.
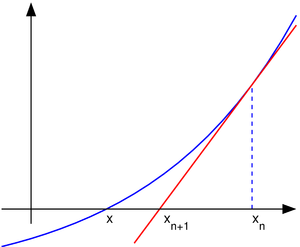
La primera de ellas es una simple interpretación geométrica. En efecto, atendiendo al desarrollo geométrico del método de la secante, podría pensarse en que si los puntos de iteración están lo suficientemente cerca (a una distancia infinitesimal), entonces la secante se sustituye por la tangente a la curva en el punto. Así pues, si por un punto de iteración trazamos la tangente a la curva, por extensión con el método de la secante, el nuevo punto de iteración se tomará como la abscisa en el origen de la tangente (punto de corte de la tangente con el eje X). Esto es equivalente a linealizar la función, es decir, f se reemplaza por una recta tal que contiene al punto (x_0, f (x_0)) y cuya pendiente coincide con la derivada de la función en el punto, f'(x_0). La nueva aproximación a la raíz, x_1, se logra la intersección de la función lineal con el eje X de abscisas. Matemáticamente:
f'(x_n)=\frac{f(x_n)}{x_n-x_{n+1}}

Una forma alternativa de obtener el algoritmo es desarrollando la función f(x) en serie de Taylor, para un entorno del punto x_n: En la ilustración adjunta del método de Newton se puede ver que x_{n+1} es una mejor aproximación que x_n para el cero (x) de la función f.

f(x)=f(x_n)+f'(x_n) (x-x_n)+ (x-x_n)^2 \frac{f''(x_n)}{2!} + ... \,
Si se trunca el desarrollo a partir del término de grado 2, y evaluamos en x_{n+1}:
f(x_{n+1})=f(x_n)+f'(x_n) (x_{n+1}-x_n) \,
Si además se acepta que x_{n+1} tiende a la raíz, se ha de cumplir que f(x_{n+1})=0, luego, sustituyendo en la expresión anterior, obtenemos el algoritmo.
Finalmente, hay que indicar que el método de Newton-Raphson puede interpretarse como un método de iteración de punto fijo. Así, dada la ecuación f(x)=0, se puede considerar el siguiente método de iteración de punto fijo:
g(x)=x+h(x) f(x) \,
Se escoge h (x) de manera que g'(r)=0 (r es la raíz buscada). Dado que g'(r) es:
g'(r)=1+h'(r) f(r) + h(r) f'(r)=1+h(r) f'(r) \,
Entonces:
h(r)=\frac{-1}{f'(r)}
Como h (x) no tiene que ser única, se escoge de la forma más sencilla:
h(x)=\frac{-1}{f'(x)}
Por tanto, imponiendo subíndices:
g(x_n)=x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}
Expresión que coincide con la del algoritmo de Newton-Raphson


Teorema de Convergencia Global del Método de Newton

Sea f\in{\mathcal{C}^2[a,b]} verificando1 :
  1. f(a) f(b)<0
  2. f'(x)\neq0 para todo x\in{[a,b]}
  3. f''(x) f''(y)\geq 0 para todo x,y\in{[a,b]}
  4. \max\left\{{\frac{\left |{f(a)}\right |}{\left |{f'(a)}\right |},\frac{\left |{f(b)}\right |}{\left |{f'(b)}\right |}}\right\}\leq b-a
Entonces existe un único s\in{[a,b]} tal que f(s)=0 por lo que la sucesión converge a s.

Estimación del Error

Se puede demostrar que el método de Newton-Raphson tiene convergencia cuadrática: si \alpha es raíz, entonces:
|x_{k+1}-\alpha|\leq C|x_k-\alpha|^2
para una cierta constante C. Esto significa que si en algún momento el error es menor o igual a 0,1, a cada nueva iteración doblamos (aproximadamente) el número de decimales exactos. En la práctica puede servir para hacer una estimación aproximada del error:
Error relativo entre dos aproximaciones sucesivas:
E = \frac{|x_{k+1}-x_k|}{|x_{k+1}|}
Con lo cual se toma el error relativo como si la última aproximación fuera el valor exacto. Se detiene el proceso iterativo cuando este error relativo es aproximadamente menor que una cantidad fijada previamente.
EJEMPLO:
Consideremos el problema de encontrar un número positivo x tal que cos(x) = x3. Podríamos tratar de encontrar el cero de f(x) = cos(x) - x3.
Sabemos que f '(x) = -sin(x) - 3x2. Ya que cos(x) ≤ 1 para todo x y x3 > 1 para x>1, deducimos que nuestro cero está entre 0 y 1. Comenzaremos probando con el valor inicial x0 = 0,5
\begin{matrix} x_1 & = & x_0 - \frac{f(x_0)}{f'(x_0)} & = & 0,5 - \frac{\cos(0,5) - 0,5^3}{-\sin(0,5) - 3 \times 0,5^2} & = & 1,112141637097 \\ x_2 & = & x_1 - \frac{f(x_1)}{f'(x_1)} & & \vdots & = & \underline{0},909672693736 \\ x_3 & & \vdots & & \vdots & = & \underline{0,86}7263818209 \\ x_4 & & \vdots & & \vdots & = & \underline{0,86547}7135298 \\ x_5 & & \vdots & & \vdots & = & \underline{0,8654740331}11 \\ x_6 & & \vdots & & \vdots & = & \underline{0,865474033102} \end{matrix}
Los dígitos correctos están subrayados. En particular, x6 es correcto para el número de decimales pedidos. Podemos ver que el número de dígitos correctos después de la coma se incrementa desde 2 (para x3) a 5 y 10, ilustando la convergencia cuadrática.



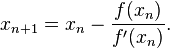
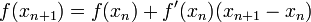
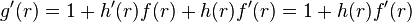
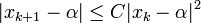
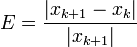
No hay comentarios:

Publicar un comentario

Nota: solo los miembros de este blog pueden publicar comentarios.

Suscribirse a: Entradas (Atom)