Bisección o Intervalo Medio
Este método , que se utiliza para resolver ecuaciones de una variable, está basado en el “Teorema de los Valores Intermedios” en el cual se establece que toda función continua f, en un intervalo cerrado [a,b], toma todos los valores que se hallan entre f(a) y f(b), de tal forma que la ecuación f(x)=0 tiene una sola raíz que verifica f(a).f(b)<0.
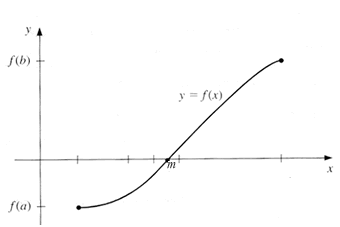
*Nota: Como observamos f(a) es negativo, por tanto el producto dará negativo, eso nos asegura que existe al menos un valor de la función que es cero.
Una vez entendido lo anterior, veamos en detalle en qué consiste el método de la bisección:
En pocas palabras, consiste en ir dividiendo la función que hemos visto arriba en subintervalos, y hallar los puntos medios de cada uno de ellos (m), quedándonos una cosa así:
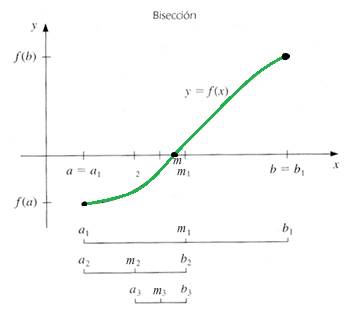
Pasos:
1) Elegimos dos valores iniciales a1 y b1, de tal forma que la función cambie de signo:
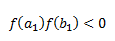
2) Realizamos la primera aproximación a la raíz, mediante la fórmula del punto medio:
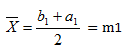
**Nota, usamos los puntos, no las funciones!! Es decir, lo que está dentro del paréntesis, NO COLOQUES aquí el resultado de sustituir en la función.
3) Ahora determinamos en que subintervalo se encuentra la raíz:
Si f(a1)f(m1) <0, entonces la raíz está en el subintervalo [a1,m1] y b1=m1
si f(a1)f(m1)>0, entonces la raíz está en el subintervalo [b1, m1] y a1=m1
Si f(a1)f(m1)=0, entonces aquí se encuentra la raíz
Resumido, hasta aquí, es ir hallando mitades sucesivamente hasta llegar al intervalo que nos de igual a cero.
4) Calculamos una nueva aproximación a la raíz.
5) Evaluamos el valor relativo aproximado:
Entonces, si:
Ejemplo: Determine el coeficiente de rozamiento c =? Necesario para que un paracaidista de masa = 68.1 kg tenga una velocidad de 40 m/s, después de una caída libre de t = 10 seg. La aceleración de la gravedad es de 9.8 m/s2. La ecuación a utilizar es:
f(c) = gm/c ( 1 - e-(c/m) t ) - v = 0
Solución analítica:
Aproximación gráfica:
f(c) = 9.8 (68.1)/c ( 1- e -(c/68.1) ) -40
= 667.38/c ( 1-e(-0.146843) ) - 40
c
|
f ( c )
|
4
|
34.115
|
8
|
17.653
|
12
|
6.067
|
16
|
-2.269
|
20
|
-8.401
|

bisección
xi = 12, xs = 16
xr = (12+16)/2 = 14, xr = xs
f(xi) = f(12) = 6.067
f(xr) = f(14) = 1.5687
f(xi) f(xr) = (6.067)( 1.5687) > 0, la raíz se encuentra en el subintervalo superior, xi = xr
n = 2
xi = 14, xs = 16 , xr = 15
f(xi) = f(14) = 1.5687
f(xr) = f(15) = -0.4248
f(xi) f(xr) = (1.5687)( -0.4248) < 0, la raíz se encuentra en este subientervalo, xs = xr
Ea = {15-14/15} x 100 = 6.667 %
n = 3
xi = 14, xs = 15 , , xr = 14.5
f(xi) = f(14) = 1.5687
f(xi) =f(14.5)= 0.5523
f(xi) f(xi) > 0, xi = xr
Ea = {14.5-15/14.5} x 100 = 3.448 %
n = 4
xi = 14.5, xs = 15 , , xr = 14.75
f(xi) = f(14.5) = 0.5523
f(xi) =f(14.75)= 0.05896
f(xi) f(xi) > 0, xi = xr
Ea = {14.75-14.5/14.75} x 100 = 1.695 %
n = 5
xi = 14.75, xs = 15 , , xr = 14.875
f(xi) = f(14.75) = 0.5896
f(xi) =f(14.87)= -0.1841
f(xi) f(xi) < 0, xs= xr
Ea = {14.875-14.75/14.875} x 100= 0.840 %
n = 6
xi = 14.75, xs = 14.875 , , xr = 14.8125
Ea = {14.8125-14.875/14.8126} x 100= 0.4219 %
Ea <
0.422% < 0.5 %
xr = 14.8125
iteración
|
Xi
|
Xs
|
Xr
|
Ea %
|
1
|
12
|
16
|
14
|
6.667
|
2
|
14
|
16
|
12
|
3.448
|
3
|
14
|
15
|
14.5
|
1.695
|
4
|
14.5
|
15
|
14.75
|
0.480
|
5
|
14.75
|
15
|
14.875
|
0.422
|
6
|
14.75
|
14.875
|
14.8125
|
Falsa Posición
Este , método utiliza una interpolación lineal ajustada a dos puntos extremos para encontrar una aproximación a la raíz. De acuerdo a la siguiente figura:

La intersección de la línea recta con el eje de la x puede estimarse:
f(xi ) = f(xs) (2.4)
xr - xi xr - xs
Reagrupando términos y reordenando
f(xi) (xr - xs) = f(xs) (xr - xi)
xr { f(xi) - f(xs) } = xs f(xi) - xi f(xs)
dividiendo entre
f(xi) - xi f(xs) =
xr = xs f(xi) - xi f(xs) (2.5)
f(xi) - f(xs)
Separando términos:
xr = xs + xs f(xi) - xi f(xs)
f(xi) - f(xs) f(xi) - f(xs)
Sumando y restando xs en el lado derecho
xr = xs + xs f(xi) - xs xi f(xs)
f(xi) - f(xs) f(xi) - f(xs)
Agrupando términos se obtiene:
xr = xs + xs f(xs) - xi f(xs)
f(xi) - f(xs) f(xi) - f(xs)
xr = xs - f(xs) (xi -xs) (2.6)
f(xi) - f(xs)
El algoritmo es idéntico al de bisección, excepto que la ec. (2.6), se usa en el paso 2.

Ejemplo
Use el método de la falsa posición, para determinar la raíz de la ecuación
f ( c ) = 667.38/c { (1-e-0.146843 c) } -40
n = 1
xi = 12 f(xi) = 6.067
xs = 16 f(xs) = -2.2687
xr = 16 - (-2.2687) (12 -16) = 14.911
6.067 - (-2.2687)
f(xr) = -0.25426
f(xi) f(xr) = 6.067 (-0.25426 ) < 0, xs = xr
n = 2
xi = 12 f(xi) = 6.067
xs = 14.9112 f(xs) = -0.25426
xr = 14.9113 - (-0.25426) (12 -14.9113) = 14.7942
6.067 - (-0.25426)
f(xr) = -0.0.2726
f(xi) f(xr) < 0, xs = xr
Ea = {(14.7942-14.9113)/14.7942} x 100% = 0.79 %
n = 3
xi = 12 f(xi) = 6.067
xs = 14.7942 f(xs) = -0.02726
xr = 14.7942 - (-0.02726) (12 -14.7942) = 14.7816
6.067 - (-0.02726)
xr = 14.7816
Ea = {(14.7816-14.7942)/14.7816} x 100% = 0.087 %
Ea < 0.087 < 0.5 %
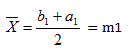
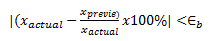
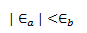
No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.